Applications de la dérivation
Extremums - Exercice 1
15 min
20
On considère la fonction définie sur par : . On note la courbe représentative de la fonction .
Question 1
Déterminer l'expression de la dérivée de puis étudier le signe de en fonction de .
Correction
est dérivable sur .
On a :
Ici la dérivée est une fonction du er degré.
Pour étudier son signe, nous allons résoudre l'inéquation .
En effet, en résolvant , on déterminera ainsi l'intervalle sur lequel la dérivée est positive ou nulle.
Il vient alors que :
équivaut successivement à
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :
On a :
Ici la dérivée est une fonction du er degré.
Pour étudier son signe, nous allons résoudre l'inéquation .
En effet, en résolvant , on déterminera ainsi l'intervalle sur lequel la dérivée est positive ou nulle.
Il vient alors que :
équivaut successivement à
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte donc que :
- si alors .
- si alors .

Question 2
Déterminer les extremums (éventuellement locaux) de sur .
Correction
- Si est négative sur alors est décroissante sur .
- Si est positive sur alors est croissante sur .
- si alors et donc est décroissante sur cet intervalle.
- si alors et donc est croissante sur cet intervalle.
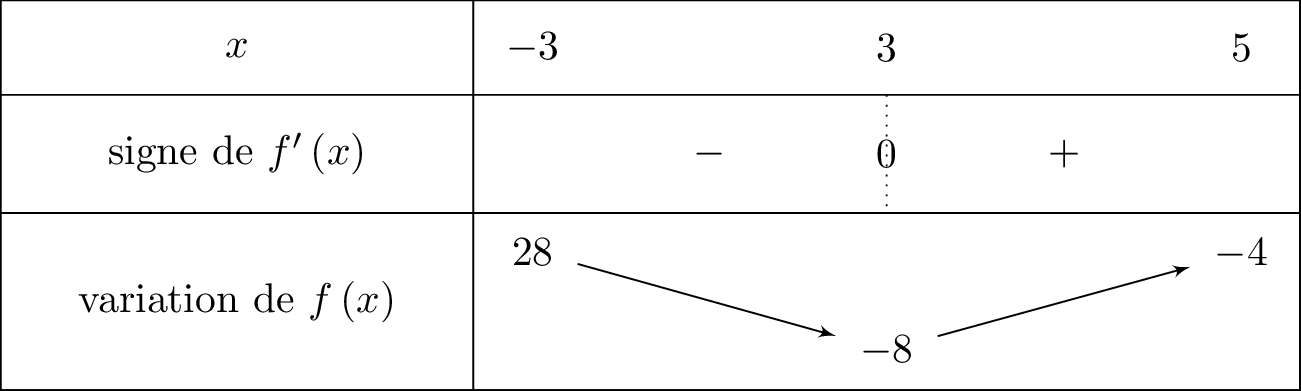
- Soit une fonction dérivable sur un intervalle et un réel de .
- Si s'annule en changeant de signe en , alors admet un extremum local en .
Question 3
La courbe admet-elle des tangentes parallèles à l'axe des abscisses ? Si oui, donner les abscisses des points vérifiant que les tangentes soient parallèles à l'axe des abscisses .
Correction
La courbe admet des tangentes parallèles à l'axe des abscisses si et seulement si s'annule.
La solution de l'équation est alors .
Il en résulte donc qu'au point d'abscisse , la courbe admet une tangente horizontale .
La solution de l'équation est alors .
Il en résulte donc qu'au point d'abscisse , la courbe admet une tangente horizontale .