Applications de la dérivation
Exercices types : ème partie - Exercice 1
15 min
25
Soit la fonction définie sur par . On note la représentation graphique de .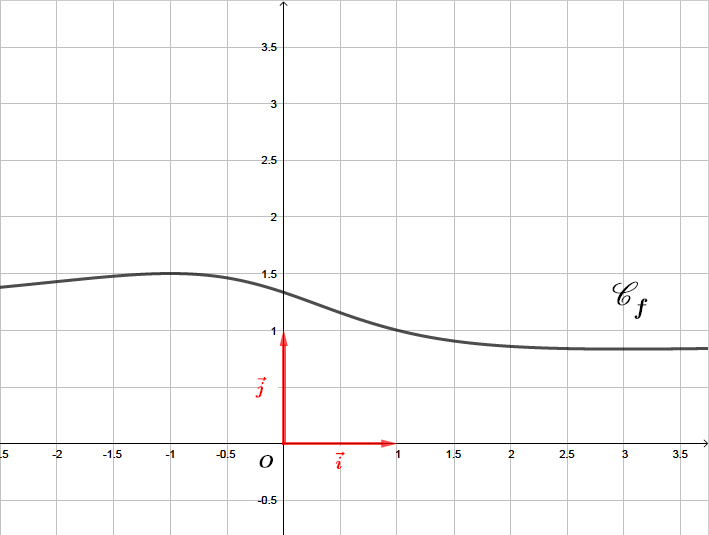

Question 1
Calculer la dérivée de .
Correction
est dérivable sur .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Question 2
Etudier les variations de .
Correction
Soit :
Pour tout réel , le dénominateur est strictement positif.
Donc, le signe de dépend du numérateur .
Or est une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et . Il est important d'indiquer que donc la parabole est tournée vers le haut. Cela explique donc pourquoi nous avons le signe de à l'extérieur des racines et le signe de à l'intérieur des racines.
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.
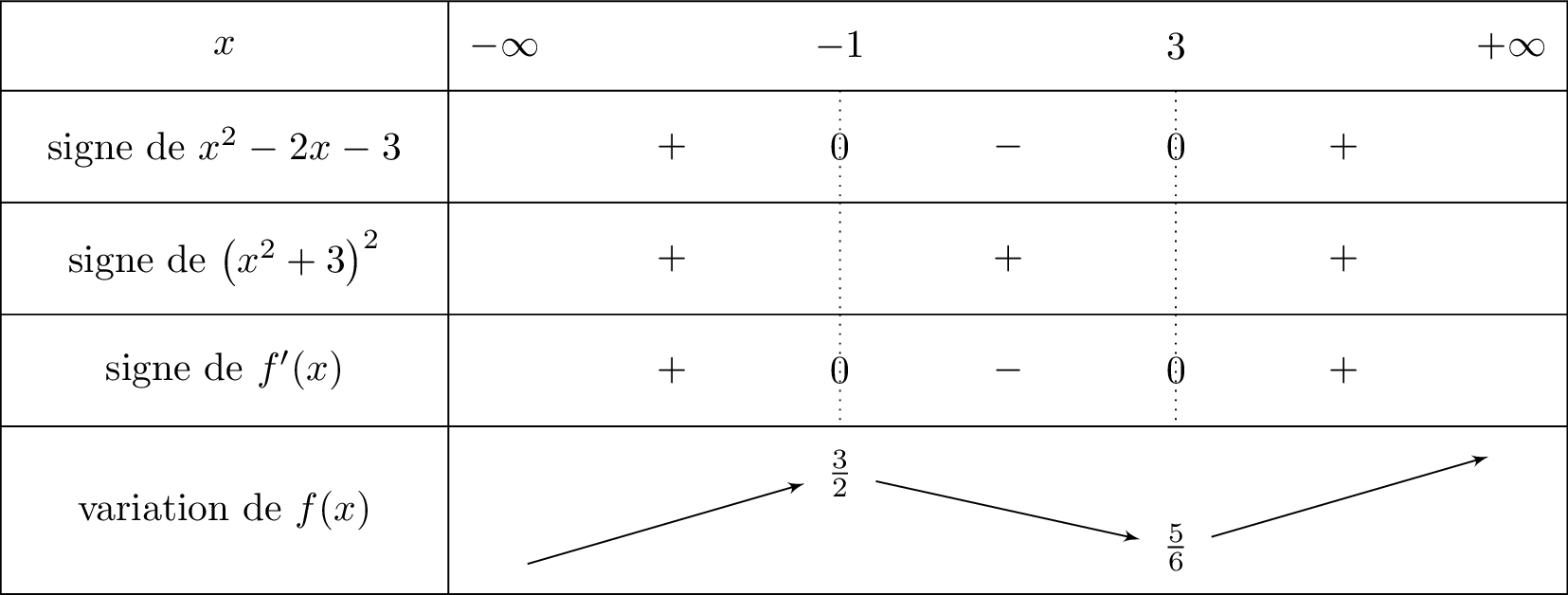 De plus:
De plus:
Pour tout réel , le dénominateur est strictement positif.
Donc, le signe de dépend du numérateur .
Or est une équation du second degré, on calcule le discriminant et on détermine les racines.
Ainsi : , il existe donc deux racines réelles distinctes telles que : et . Il est important d'indiquer que donc la parabole est tournée vers le haut. Cela explique donc pourquoi nous avons le signe de à l'extérieur des racines et le signe de à l'intérieur des racines.
On en déduit le tableau de signe de ainsi que le tableau de variation de . On indiquera les valeurs des extrema.

Question 3
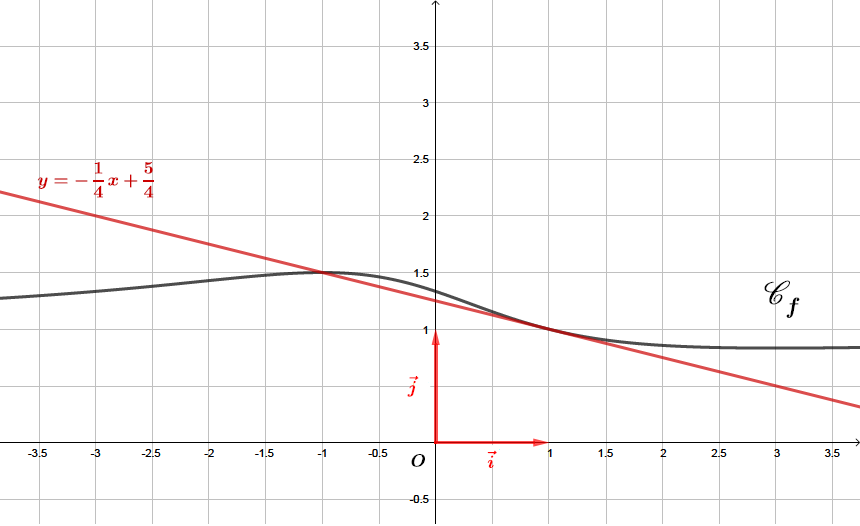
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors .