Variations des fonctions associées
Exercices types - Exercice 1
1 min
0
Question 1
Soit une fonction définie sur l'intervalle dont on donne le tableau de variation ci-dessous:
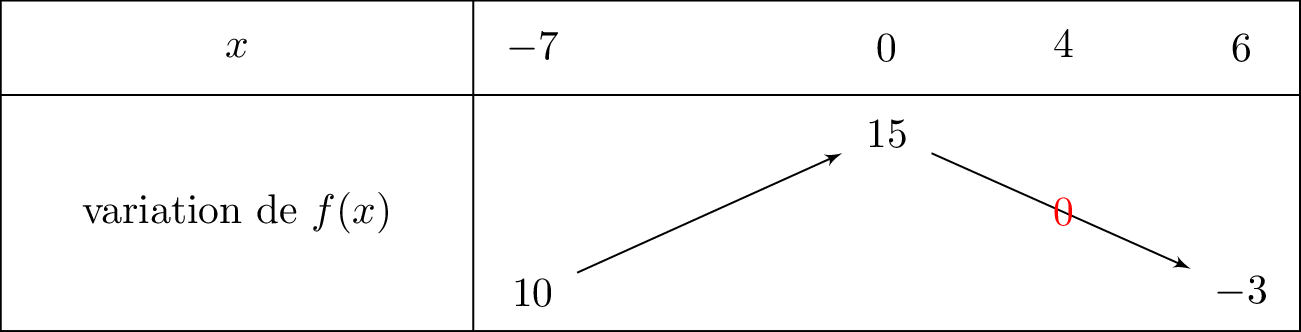

Dresser le tableau de variation de la fonction définie par : . Vous devrez justifier.
Correction
- Soit un réel négatif, alors les fonctions et ont des sens de variations contraires.
- Soit un réel positif , alors les fonctions et ont des sens de variations identiques.
La fonction est croissante sur l'intervalle donc la fonction est décroissante sur
La fonction est décroissante sur l'intervalle donc la fonction est croissante sur
De plus :
donc
donc
donc
On résume maintenant cela dans le tableau de variation pour la fonction :
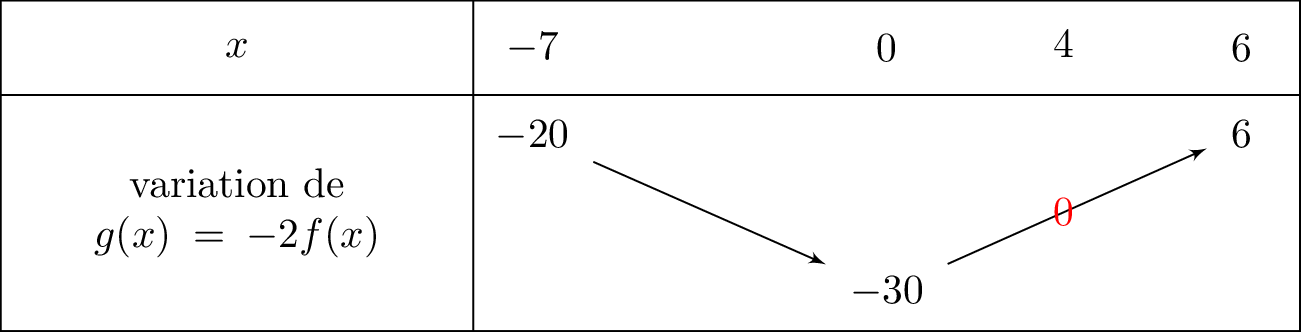
Question 2
Dresser le tableau de variation de la fonction définie par : . Vous devrez justifier.
Correction
- Soit un réel , alors les fonctions et ont des sens de variations identiques.
La fonction est croissante sur l'intervalle donc la fonction est croissante sur
La fonction est décroissante sur l'intervalle donc la fonction est décroissante sur
De plus :
donc
donc
donc
donc
On résume maintenant cela dans le tableau de variation pour la fonction :
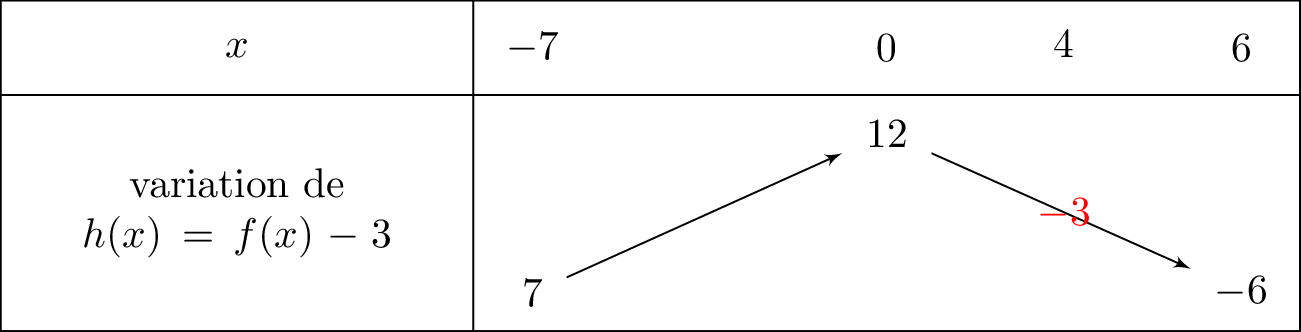
Question 3
Sur quel intervalle la fonction définie par
Correction
La fonction est définie lorsque est positive. D'après le tableau de variation de , on remarque que la fonction est positive sur l'intervalle .
Il en résulte que le domaine de définition de la fonction est l'intervalle
Il en résulte que le domaine de définition de la fonction est l'intervalle
Question 4
Dresser le tableau de variation de la fonction définie par : . Vous devrez justifier.
Correction
D'après la question précédente, le domaine de définition de la fonction est l'intervalle .
La fonction est croissante sur l'intervalle donc la fonction est croissante sur
La fonction est décroissante sur l'intervalle donc la fonction est décroissante sur
De plus :
donc
donc
donc
On résume maintenant cela dans le tableau de variation pour la fonction :
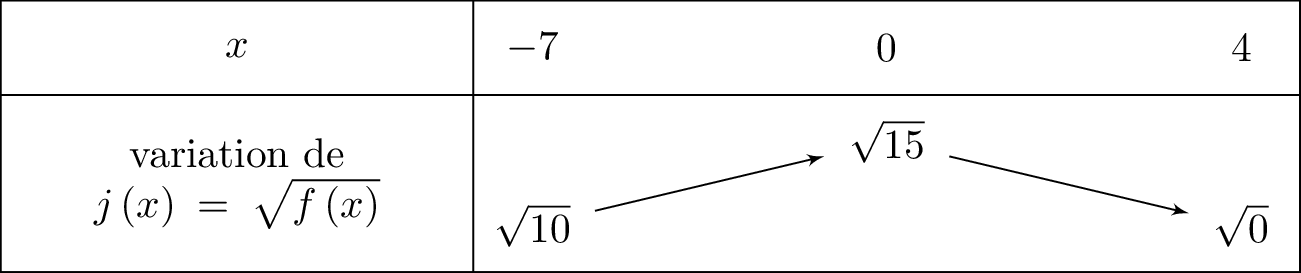
- Soit un intervalle où la fonction est positive. Alors les fonctions et ont des sens de variations identiques.
La fonction est décroissante sur l'intervalle donc la fonction est décroissante sur
De plus :
donc
donc
donc
On résume maintenant cela dans le tableau de variation pour la fonction :

Question 5
Sur quel intervalle la fonction définie par
Correction
La fonction est définie lorsque ne s'annule pas. Or, d'après le tableau de variation de , on remarque que la fonction s'annule pour .
Il en résulte que le domaine de définition de la fonction est l'intervalle
Il en résulte que le domaine de définition de la fonction est l'intervalle
Question 6
Dresser le tableau de variation de la fonction définie par : . Vous devrez justifier.
Correction
D'après la question précédente, le domaine de définition de la fonction est l'intervalle .
La fonction est croissante sur l'intervalle donc la fonction est décroissante sur
La fonction est décroissante sur l'intervalle donc la fonction est croissante sur
La fonction est décroissante sur l'intervalle donc la fonction est croissante sur
De plus :
donc
donc
donc
Pour , nous aurons donc une valeur interdite modélisée par une double barre.
On résume maintenant cela dans le tableau de variation pour la fonction :
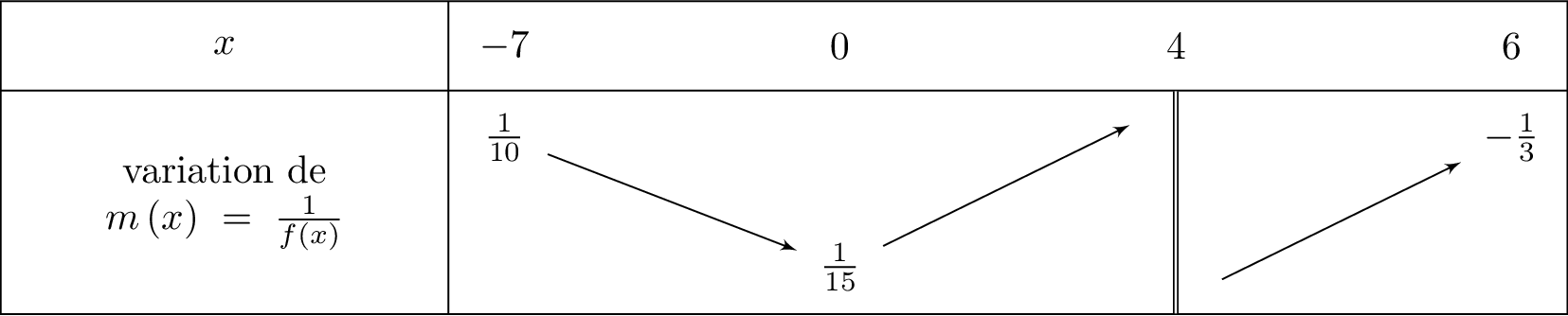
- Soit un intervalle où la fonction ne s'annule pas. Alors les fonctions et ont des sens de variations contraires.
La fonction est décroissante sur l'intervalle donc la fonction est croissante sur
La fonction est décroissante sur l'intervalle donc la fonction est croissante sur
De plus :
donc
donc
donc
Pour , nous aurons donc une valeur interdite modélisée par une double barre.
On résume maintenant cela dans le tableau de variation pour la fonction :
