Variations des fonctions associées
Décomposition et variation des fonctions associées - Exercice 1
1 min
0
Question 1
Décomposer les fonctions suivantes à l'aide de fonctions usuelles.
Vous devrez choisir ensuite des intervalles pour en déduire le sens de variations de .
Vous devrez choisir ensuite des intervalles pour en déduire le sens de variations de .
Correction
est définie pour toutes les valeurs réelles sauf celles qui annulent le dénominateur de .
La valeur interdite est celle qui annule le dénominateur .
Ainsi d'où .
Le domaine de définition est : .
Etudions, d'une part, le sens de variation de sur l'intervalle .
On décompose la fonction en avec et .
Pour tout , la fonction est croissante car il s'agit d'une fonction affine dont le coefficient directeur est positif.
La fonction est définie lorsque , ce qui est vrai sur l'intervalle .
Ainsi, pour tout , la fonction a un sens de variation contraire à celui de la fonction .
Donc la fonction est décroissante sur .
De plus, la fonction a un sens de variation contraire à celui de la fonction car
Donc la fonction est croissante sur .
Il en résulte que la fonction est croissante sur .
Finalement, la fonction est croissante sur .
Etudions, d'autre part, le sens de variation de sur l'intervalle .
On décompose la fonction en avec et .
Pour tout , la fonction est croissante car il s'agit d'une fonction affine dont le coefficient directeur est positif.
La fonction est définie lorsque , ce qui est vrai sur l'intervalle .
Ainsi, pour tout , la fonction a un sens de variation contraire à celui de la fonction .
Donc la fonction est décroissante sur .
De plus, la fonction a un sens de variation contraire à celui de la fonction car
Donc la fonction est croissante sur .
Il en résulte que la fonction est croissante sur .
Finalement, la fonction est croissante sur .
Nous résumons cela dans un tableau de variation :
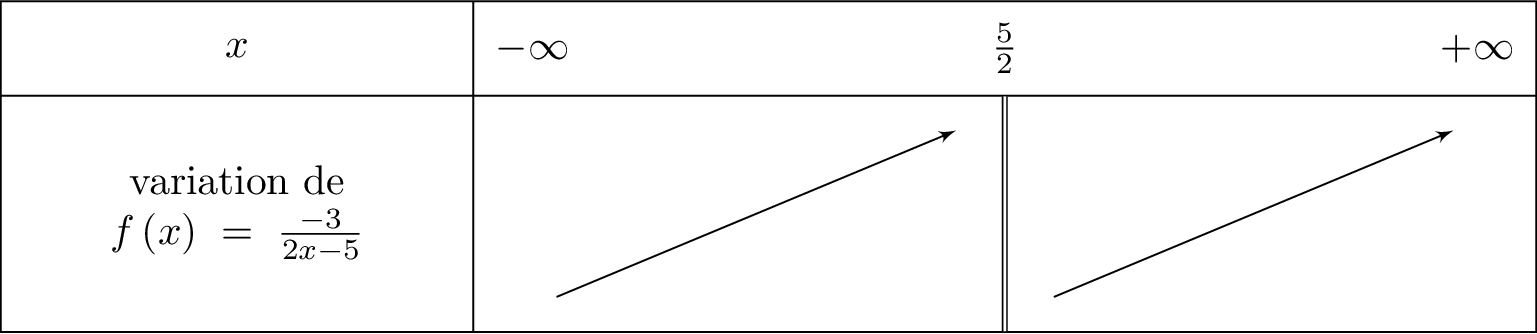
La valeur interdite est celle qui annule le dénominateur .
Ainsi d'où .
Le domaine de définition est : .
Etudions, d'une part, le sens de variation de sur l'intervalle .
On décompose la fonction en avec et .
Pour tout , la fonction est croissante car il s'agit d'une fonction affine dont le coefficient directeur est positif.
La fonction est définie lorsque , ce qui est vrai sur l'intervalle .
- Soit un intervalle où la fonction ne s'annule pas. Alors les fonctions et ont des sens de variations contraires.
Donc la fonction est décroissante sur .
De plus, la fonction a un sens de variation contraire à celui de la fonction car
Donc la fonction est croissante sur .
Il en résulte que la fonction est croissante sur .
Finalement, la fonction est croissante sur .
Etudions, d'autre part, le sens de variation de sur l'intervalle .
On décompose la fonction en avec et .
Pour tout , la fonction est croissante car il s'agit d'une fonction affine dont le coefficient directeur est positif.
La fonction est définie lorsque , ce qui est vrai sur l'intervalle .
Ainsi, pour tout , la fonction a un sens de variation contraire à celui de la fonction .
Donc la fonction est décroissante sur .
- Soit un réel négatif, alors les fonctions et ont des sens de variations contraires.
- Soit un réel positif , alors les fonctions et ont des sens de variations identiques.
Donc la fonction est croissante sur .
Il en résulte que la fonction est croissante sur .
Finalement, la fonction est croissante sur .
Nous résumons cela dans un tableau de variation :

Question 2
Correction
La fonction est définie pour toutes les valeurs réelles qui rendent le radical positif ou nul.
Le radical correspond à l'expression qui est sous la racine carrée.
est définie si , et seulement si : .
Ainsi :
L'ensemble de définition de la fonction est :
Nous allons donc étudier les variations de la fonction sur
Pour les variations, on décompose la fonction en avec ; et .
La fonction est une fonction affine de coefficient directeur . La fonction est donc croissante sur .
Comme les fonctions et ont les mêmes variations, la fonction est croissante sur .
Ensuite : et ont de sens de variations contraires car . Ainsi la fonction est décroissante sur .
Enfin : et ont les mêmes sens de variations (ici ) . Finalement, la fonction est décroissante sur .
Il en résulte que la fonction est décroissante sur .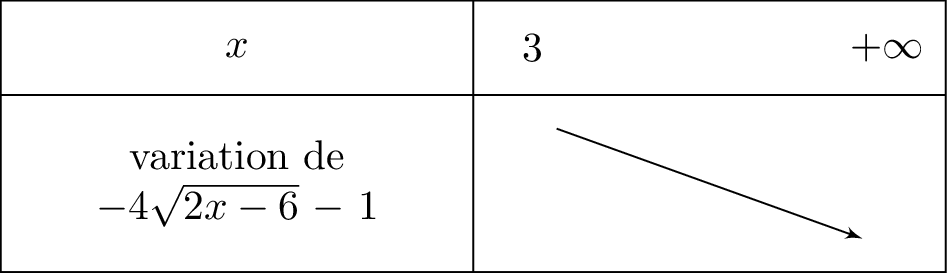
Le radical correspond à l'expression qui est sous la racine carrée.
est définie si , et seulement si : .
Ainsi :
L'ensemble de définition de la fonction est :
.
Nous allons donc étudier les variations de la fonction sur
Pour les variations, on décompose la fonction en avec ; et .
La fonction est une fonction affine de coefficient directeur . La fonction est donc croissante sur .
- Racine carré
- Soit une fonction positive sur , alors les fonctions et ont les mêmes variations.
- Soit un réel négatif, alors les fonctions et ont des sens de variations contraires.
- Soit un réel positif , alors les fonctions et ont des sens de variations identiques.
- Soit un réel , alors les fonctions et ont des sens de variations identiques.
Il en résulte que la fonction est décroissante sur .

Question 3
Correction
Nous avons une racine carrée et de plus la racine carrée est au dénominateur. Il faut donc que : et . Autrement dit, est définie si, et seulement si,
Ainsi :
L'ensemble de définition de la fonction est :
Nous allons donc étudier les variations de la fonction sur
Pour les variations, on décompose la fonction en avec et .
La fonction est une fonction affine de coefficient directeur . La fonction est donc décroissante sur .
Comme les fonctions et ont les mêmes variations, la fonction est croissante sur .
La fonction est définie lorsque , ce qui est vrai sur l'intervalle .
Ainsi, pour tout , la fonction a un sens de variation contraire à celui de la fonction .
Donc la fonction est décroissante sur . Autrement dit, la fonction est décroissante sur .
Ensuite : et ont de sens de variations contraires car . Ainsi la fonction est croissante sur .
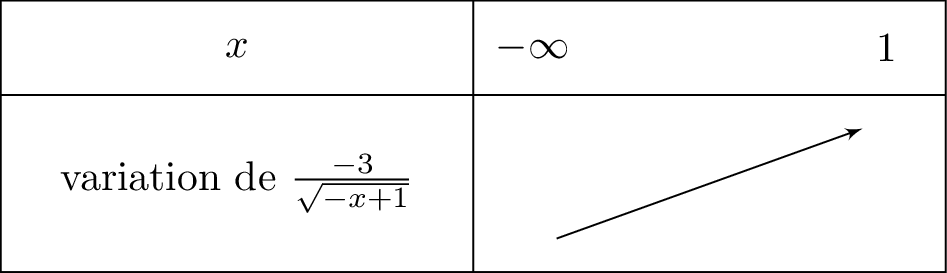
Ainsi :
L'ensemble de définition de la fonction est :
.
Nous allons donc étudier les variations de la fonction sur
Pour les variations, on décompose la fonction en avec et .
La fonction est une fonction affine de coefficient directeur . La fonction est donc décroissante sur .
- Racine carré
- Soit une fonction positive sur , alors les fonctions et ont les mêmes variations.
La fonction est définie lorsque , ce qui est vrai sur l'intervalle .
- Fonction inverse
- Soit un intervalle où la fonction ne s'annule pas. Alors les fonctions et ont des sens de variations contraires.
Donc la fonction est décroissante sur . Autrement dit, la fonction est décroissante sur .
- Soit un réel négatif, alors les fonctions et ont des sens de variations contraires.
- Soit un réel positif , alors les fonctions et ont des sens de variations identiques.
