Produit scalaire

Produit Scalaire : définition par le projeté orthogonal - Exercice 1

10 min
20
Question 1
Le quadrillage des petits carreaux sont de mesure 11 .

Calculer AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC}

Correction
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
    • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires mais ont des sens opposés.
Il vient alors que :
AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
AB→⋅AC→=−5×2\overrightarrow{AB} \cdot \overrightarrow{AC} =-5\times 2
AB→⋅AC→=−10\overrightarrow{AB} \cdot \overrightarrow{AC} =-10
Question 2

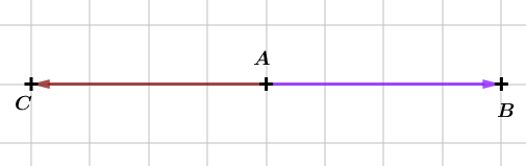
Calculer AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC}

Correction
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
    • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires mais ont des sens opposés.
Il vient alors que :
AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
AB→⋅AC→=−4×4\overrightarrow{AB} \cdot \overrightarrow{AC} =-4\times 4
AB→⋅AC→=−16\overrightarrow{AB} \cdot \overrightarrow{AC} =-16
Question 3

Calculer 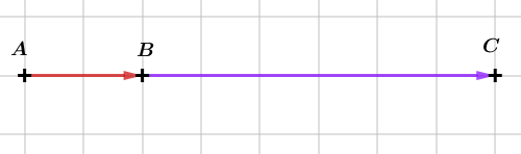AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC}

Correction
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
    • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Les vecteurs AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens.
Il vient alors que :
AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
AB→⋅AC→=2×8\overrightarrow{AB} \cdot \overrightarrow{AC} =2\times 8
AB→⋅AC→=16\overrightarrow{AB} \cdot \overrightarrow{AC} =16
Question 4

Calculer 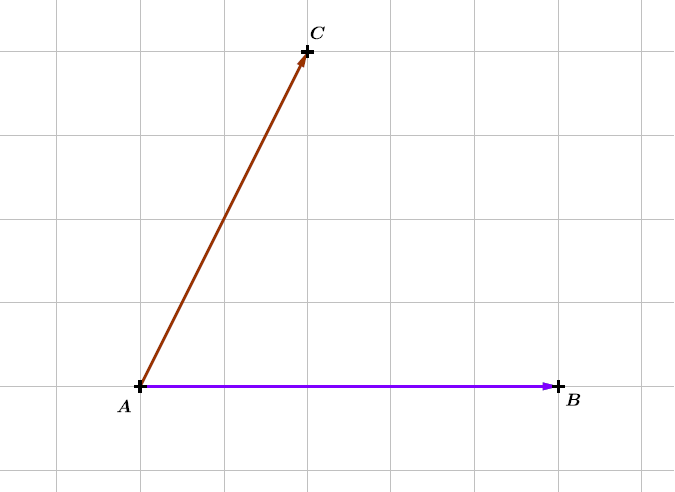AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC}

Correction
Soient AB→\overrightarrow{AB} et AC→\overrightarrow{AC} deux vecteurs non nuls.
Soit H\red{H} le projeté orthogonal de C\blue{C} sur la droite (AB)\left(AB\right).
Il vient alors que : AB→⋅AC→=AB→⋅AH→\overrightarrow{AB} \cdot \overrightarrow{A\blue{C}}=\overrightarrow{AB} \cdot \overrightarrow{A\red{H}}
Soit HH le projeté orthogonal de CC sur la droite (AB)\left(AB\right) . Il en résulte donc que :
AB→⋅AC→=AB→⋅AH→\overrightarrow{AB} \cdot \overrightarrow{AC}=\overrightarrow{AB} \cdot \overrightarrow{AH}
Les vecteurs AB→\overrightarrow{AB} et AH→\overrightarrow{AH} sont colinéaires et de même sens.
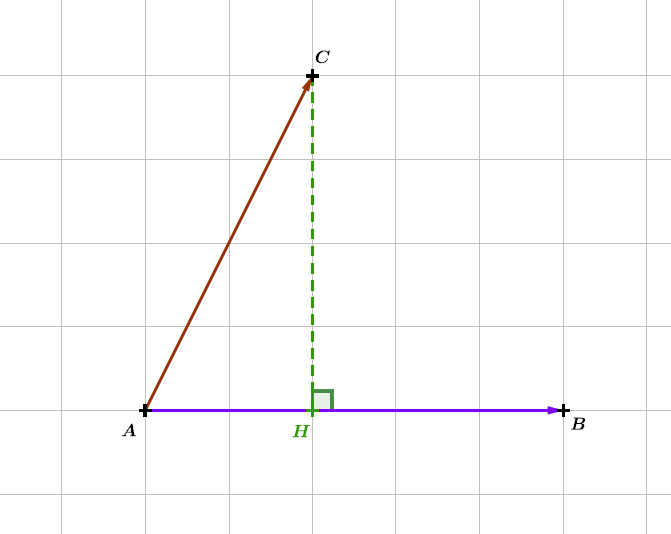
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
    • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Il vient alors que :
AB→⋅AC→=AB→⋅AH→=AB×AH\overrightarrow{AB} \cdot \overrightarrow{AC} =\overrightarrow{AB} \cdot \overrightarrow{AH}=AB\times AH
AB→⋅AC→=5×2\overrightarrow{AB} \cdot \overrightarrow{AC} =5\times 2
AB→⋅AC→=10\overrightarrow{AB} \cdot \overrightarrow{AC} =10
Question 5

Calculer 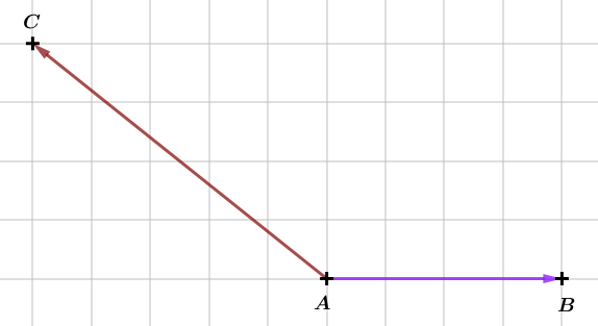AB→⋅AC→\overrightarrow{AB} \cdot \overrightarrow{AC}

Correction
Soient AB→\overrightarrow{AB} et AC→\overrightarrow{AC} deux vecteurs non nuls.
Soit H\red{H} le projeté orthogonal de C\blue{C} sur la droite (AB)\left(AB\right).
Il vient alors que : AB→⋅AC→=AB→⋅AH→\overrightarrow{AB} \cdot \overrightarrow{A\blue{C}}=\overrightarrow{AB} \cdot \overrightarrow{A\red{H}}
Soit HH le projeté orthogonal de CC sur la droite (AB)\left(AB\right) . Il en résulte donc que :
AB→⋅AC→=AB→⋅AH→\overrightarrow{AB} \cdot \overrightarrow{AC}=\overrightarrow{AB} \cdot \overrightarrow{AH}
Les vecteurs AB→\overrightarrow{AB} et AH→\overrightarrow{AH} sont colinéaires mais de sens opposés.
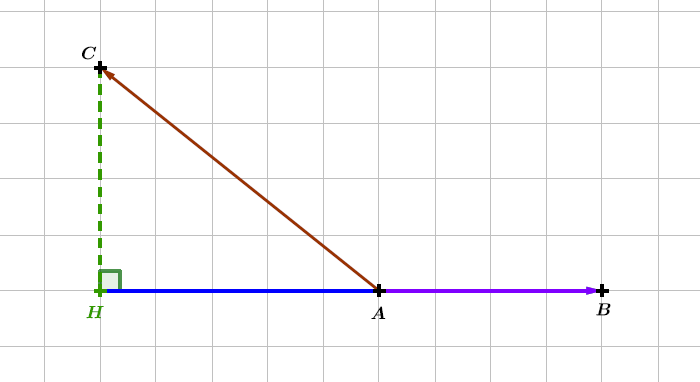
  • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de même sens alors : AB→⋅AC→=AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =AB\times AC
    • Si AB→\overrightarrow{AB} et AC→\overrightarrow{AC} sont colinéaires et de sens opposés alors : AB→⋅AC→=−AB×AC\overrightarrow{AB} \cdot \overrightarrow{AC} =-AB\times AC
Il vient alors que :
AB→⋅AC→=AB→⋅AH→=−AB×AH\overrightarrow{AB} \cdot \overrightarrow{AC} =\overrightarrow{AB} \cdot \overrightarrow{AH}=-AB\times AH
AB→⋅AC→=−4×5\overrightarrow{AB} \cdot \overrightarrow{AC} =-4\times 5
AB→⋅AC→=−20\overrightarrow{AB} \cdot \overrightarrow{AC} =-20