Probabilités
Loi binomiale - Exercice 1
1 min
0
Question 1
Un ami vous propose le jeu suivant : vous lancez deux fois de suite une pièce de monnaie.
Si vous obtenez "deux piles" vous gagnez euros. Si vous obtenez " pile" vous gagnez euros. Sinon vous perdez euros.
Jouez-vous? Justifier votre choix?
Correction
On traduit l'énoncé à l'aide d'un arbre, que l'on donne ci-dessous :
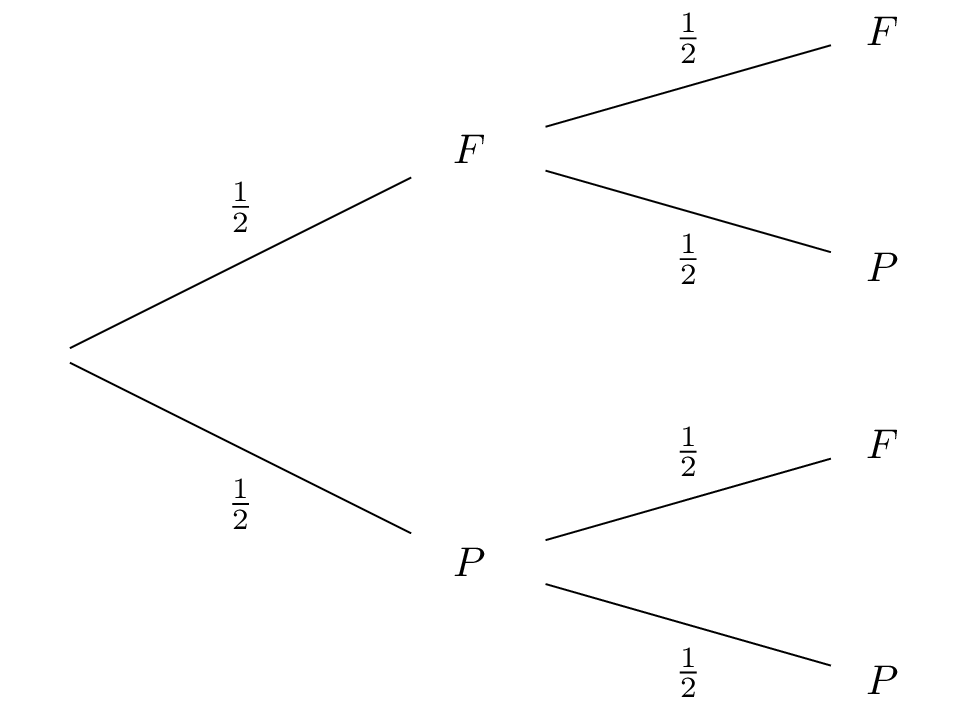
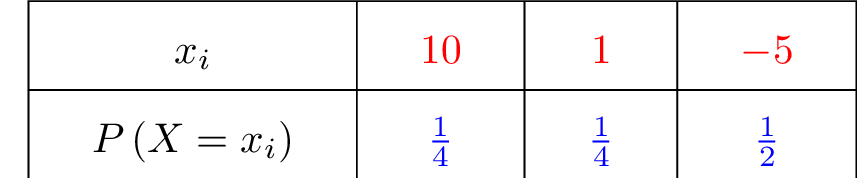
Notons la variable aléatoire qui associe le gain (positif ou négatif). Dressons dans ce cas, la loi de probabilité de . Il vient alors que :
 Nous allons maintenant calculer l’espérance mathématique de la variablede
Nous allons maintenant calculer l’espérance mathématique de la variablede
Ainsi :
En moyenne, une personne gagnera en moyenne euros.

Notons la variable aléatoire qui associe le gain (positif ou négatif). Dressons dans ce cas, la loi de probabilité de . Il vient alors que :

On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Ainsi :
En moyenne, une personne gagnera en moyenne euros.
Question 2
Cette fois ci, votre ami vous propose le jeu suivant : vous lancez fois de suite une pièce de monnaie.
Si vous obtenez "six piles" vous gagnez euros. Sinon vous perdez euros.
Calculer la probabilités de réussir les piles lors des lancers.
Correction
Dans cette partie, il est impossible de générer un arbre car il sera trop grand. Vous aurez branches c'est à dire branches....
Cette expérience peut se ramener à la loi binomiale pourvu que l’on lance le dé toujours de la même façon. Les expériences sont indépendantes et chaque expérience a deux issues :
Soit on fait pile avec une probabilité , qui correspond ici au succès. Soit on fait face avec une probabilité , qui correspond ici à l'échec. On a donc une loi binomiale de paramètres et que l'on écrit : .
Notons la variable aléatoire qui associe le nombre de piles dans le jeu. Ainsi, pour avoir piles, il nous faut donc calculer :
Ainsi à la calculatrice, on obtient :
Cette expérience peut se ramener à la loi binomiale pourvu que l’on lance le dé toujours de la même façon. Les expériences sont indépendantes et chaque expérience a deux issues :
- Dans un schéma de Bernoulli d’ordre et de paramètre , la loi de probabilité de la variable aléatoire qui à chaque issue associe le nombre de succès est définie par :
On dit alors que la variable aléatoire suit une loi binomiale
Ainsi à la calculatrice, on obtient :
Question 3
Calculer la probabilité de perdre.
Correction
Notons l'évènement "ne pas réussir à faire les piles."
est donc l'évènement contraire de réussir à faire les piles.
est donc l'évènement contraire de réussir à faire les piles.
On appelle événement contraire d’un événement , l’événement noté tel que :
Il en résulte donc que :Question 4
Jouez-vous? Justifier votre choix?
Correction
Nous allons dresser, ci-dessous, la loi de probabilité de la variable qui correspond au gain possible pour le jeu.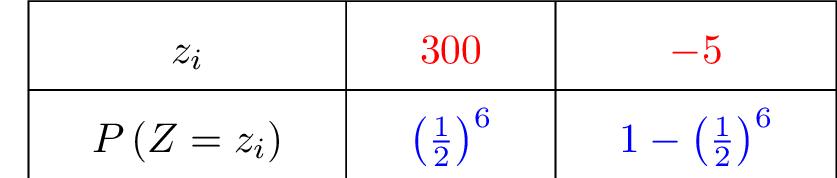
Ainsi :
En moyenne, une personne perdra en moyenne euros.
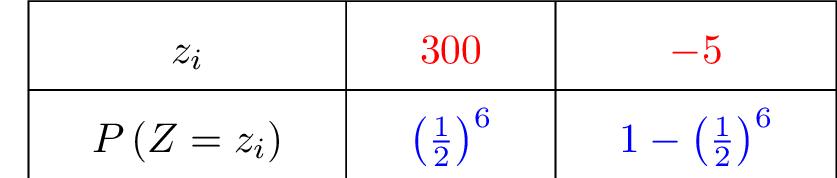
On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Ainsi :
En moyenne, une personne perdra en moyenne euros.