Angles orientés
Sous forme de petits problèmes - Exercice 1
20 min
40
est un triangle rectangle en de sens direct tel que et est un triangle équilatéral de sens direct.
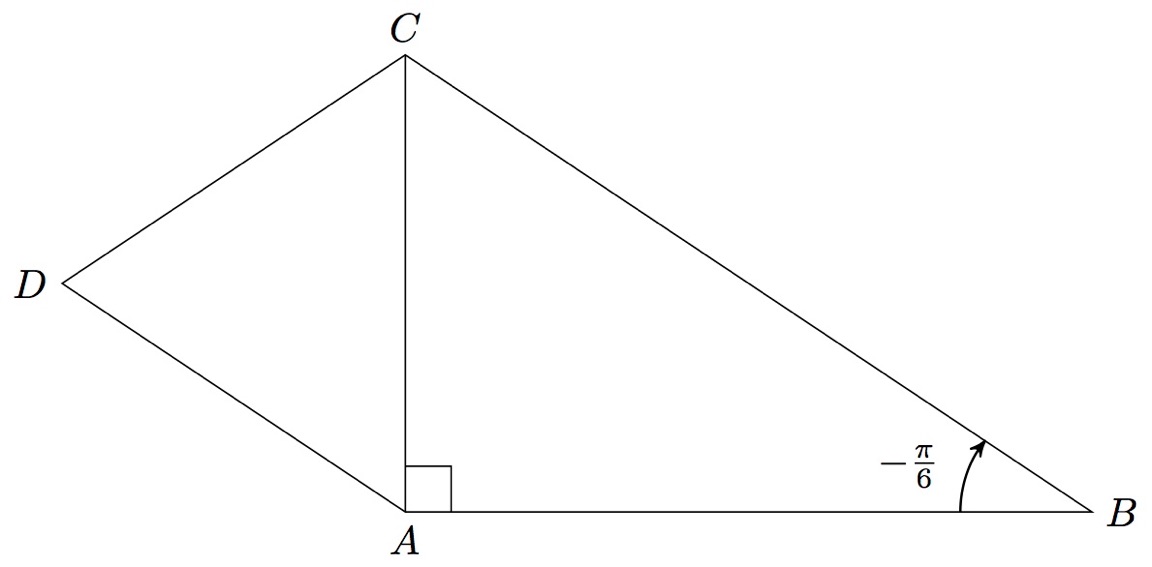 Déterminer la mesure principale des angles orientés suivants :
Déterminer la mesure principale des angles orientés suivants :

Question 1
Correction
D'une part, les angles du triangle , ils sont tous égaux à car est un triangle équilatéral.
D'autre part, nous allons calculer tous les angles du triangle .
Nous ne tiendrons pas compte du sens direct pour les calculer.
La mesure de l'angle est et celle de l'angle est or on sait que la somme des trois angles d'un triangle vaut .
Ainsi :
soit .
L'angle est dans le sens direct donc :
D'autre part, nous allons calculer tous les angles du triangle .
Nous ne tiendrons pas compte du sens direct pour les calculer.
La mesure de l'angle est et celle de l'angle est or on sait que la somme des trois angles d'un triangle vaut .
Ainsi :
soit .
L'angle est dans le sens direct donc :
Question 2
Correction
L'angle est dans le sens indirect.
d'après la relation de Chasles.
Ainsi :
d'après la relation de Chasles.
Ainsi :
Question 3
Correction
Soient les vecteurs et on a alors :
De cette manière les deux vecteurs ont bien la même origine .L'angle est dans le sens indirect.
Ainsi :
Question 4
Correction
d'après la relation de Chasles.
Ensuite, n'oubliez pas que les vecteurs qui composent un angle orienté doivent avoir la même origine.
D'où :
On va donner la mesure principale de .
Ainsi : soit :
Ensuite, n'oubliez pas que les vecteurs qui composent un angle orienté doivent avoir la même origine.
D'où :
Soient les vecteurs et on a alors :
On va donner la mesure principale de .
Ainsi : soit :