Produit scalaire
ÉPREUVES COMMUNES DE CONTRÔLE CONTINU : ère partie - Exercice 1
20 min
40
Soit un repère orthonormé.
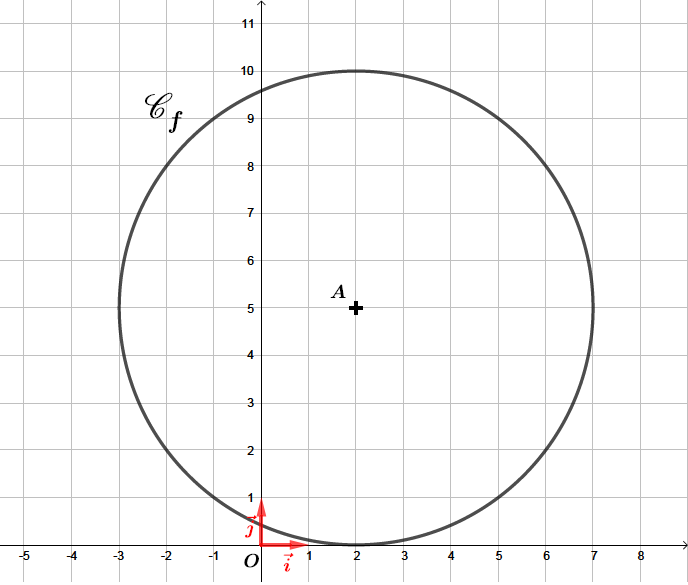
On considère le cercle de centre et de rayon .
On considère le cercle de centre et de rayon .
Question 1
Montrer qu'une équation du cercle est : .
Correction
- L'équation d'un cercle de centre et de rayon , dans un repère orthonormé est :
Nous allons développer maintenant l'expression, ce qui donne :
Ainsi :
Question 2
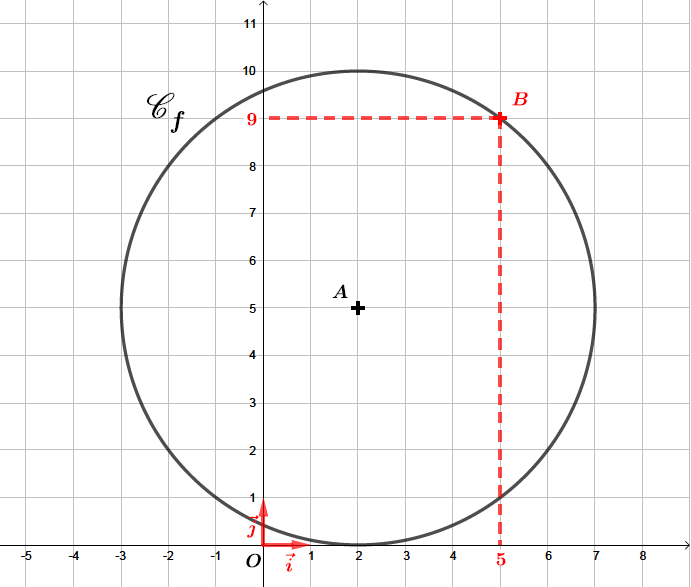
Vérifier que le point appartient à ce cercle.
Correction
Nous allons donc calculer .
Il vient alors que :
Ainsi :
Le point appartient bien au cercle d'équation .
Question 3
Que peut-on dire de la tangente au cercle au point et de la droite ?
Correction
La tangente à un cercle de centre en un point de est la droite passant par et perpendiculaire au rayon .
Question 4
Déterminer une équation de la tangente au cercle au point .
Correction
Soit un point appartenant à la tangente au cercle au point .
D'après la question , on peut affirmer que la droite et la droite sont perpendiculaires.
Il en résulte donc que :
Il nous calculer les vecteurs et , d'où :
D'après la question , on peut affirmer que la droite et la droite sont perpendiculaires.
Il en résulte donc que :
Il nous calculer les vecteurs et , d'où :
- Dans un repère orthonormé , le produit scalaire de deux vecteurs et de coordonnées respectives et est égal à :
Ainsi :
Une équation de la tangente au cercle au point est alors :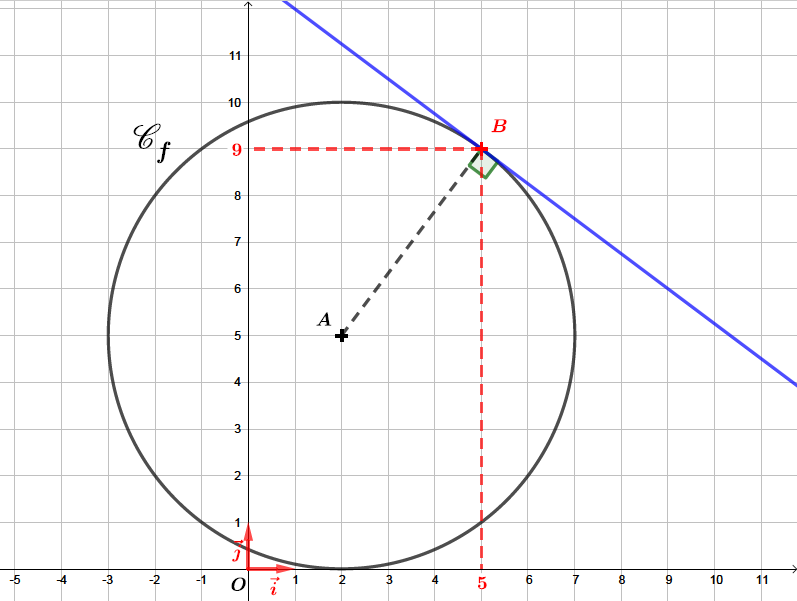
Question 5
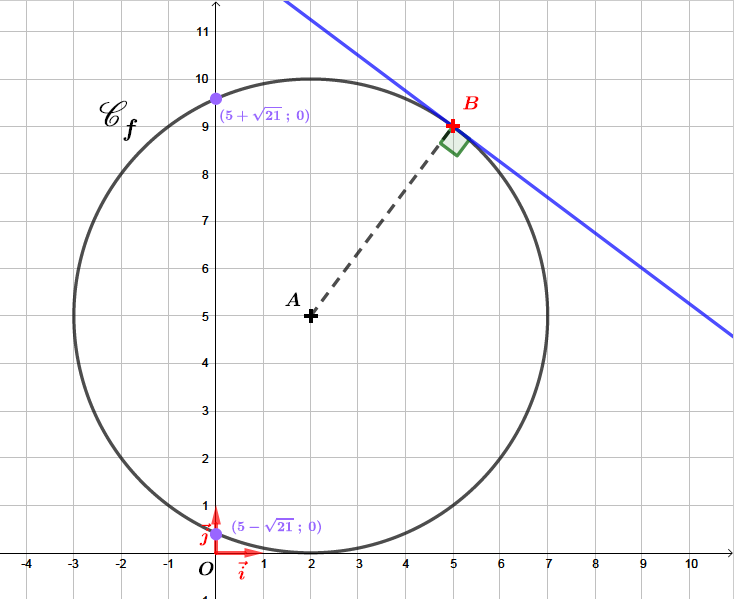
Calculer les coordonnées des points d’intersection du cercle avec l’axe des ordonnées.
Correction
Les points d’intersection du cercle avec l’axe des ordonnées ont une abscisse nulle. Autrement dit : .
Il vient alors que :
Il faut donc résoudre l'équation
Calcul du discriminant
Ainsi :
Comme alors l'équation admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
Le cercle a deux points communs avec l’axe des ordonnées de coordonnées : et
Il vient alors que :
Il faut donc résoudre l'équation
Calcul du discriminant
Ainsi :
Comme alors l'équation admet deux racines réelles distinctes notées et telles que :
ainsi d'où
ainsi d'où
Le cercle a deux points communs avec l’axe des ordonnées de coordonnées : et
