Fonctions trigonométriques

cos⁡2(x)+sin⁡2(x)=1\cos ^{2} \left(x\right)+\sin ^{2} \left(x\right)=1 - Exercice 1

20 min
35
Soit xx un réel de l'intervalle [π2;π]\left[\frac{\pi }{2} ;\pi \right] tel que sin⁡(x)=13\sin \left(x\right)=\frac{1}{3}
Question 1

Calculer cos⁡(x)\cos \left(x\right)

Correction
Pour tout réel xx, on a : cos⁡2(x)+sin⁡2(x)=1\cos ^{2} \left(x\right)+\sin ^{2} \left(x\right)=1
On sait que :
cos⁡2(x)+sin⁡2(x)=1\cos ^{2} \left(x\right)+\sin ^{2} \left(x\right)=1 équivaut successivement à :
cos⁡2(x)+(13)2=1\cos ^{2} \left(x\right)+\left(\frac{1}{3} \right)^{2} =1 car sin⁡(x)=13\sin \left(x\right)=\frac{1}{3}
cos⁡2(x)+19=1\cos ^{2} \left(x\right)+\frac{1}{9} =1
cos⁡2(x)=1−19\cos ^{2} \left(x\right)=1-\frac{1}{9}
cos⁡2(x)=99−19\cos ^{2} \left(x\right)=\frac{9}{9} -\frac{1}{9}
cos⁡2(x)=89\cos ^{2} \left(x\right)=\frac{8}{9}
Ainsi : cos⁡(x)=89\cos \left(x\right)=\sqrt{\frac{8}{9} } ou cos⁡(x)=−89\cos \left(x\right)=-\sqrt{\frac{8}{9} }
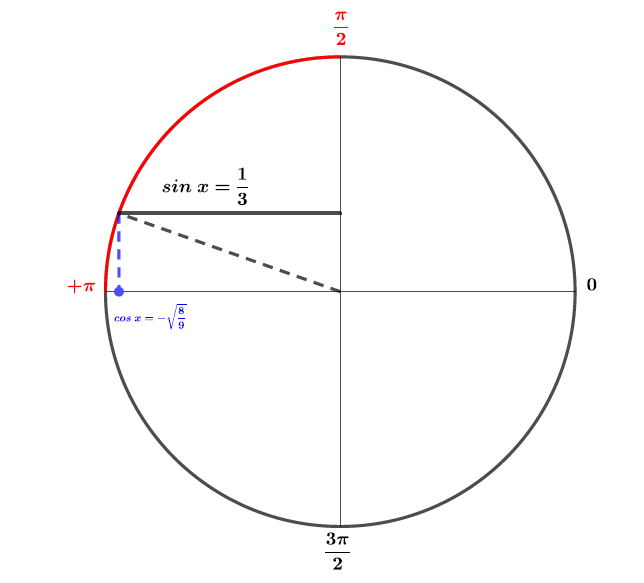
Or x∈[π2;π]x\in \left[\frac{\pi }{2} ;\pi \right]. Cela signifie que le cosinus doit être négatif.
On ne garde alors que cos⁡(x)=−89\cos \left(x\right)=-\sqrt{\frac{8}{9} } .
En effet, sur l'intervalle [π2;π]\left[\frac{\pi }{2} ;\pi \right] le cosinus est négatif.
Question 2

En déduire : cos⁡(x+π)\cos \left(x+\pi \right) ; sin⁡(π−x)\sin \left(\pi -x\right) ; sin⁡(π2−x)\sin \left(\frac{\pi }{2} -x\right) ; cos⁡(π2+x)\cos \left(\frac{\pi }{2} +x\right) ; cos⁡(x+2π)\cos \left(x+2\pi \right)

Correction
  • D'après le cours, on sait que : cos⁡(x+π)=−cos⁡(x)\cos \left(x+\pi \right)=-\cos \left(x\right)
    Ainsi : cos⁡(x+π)=−cos⁡(x)=−(−89)=89\cos \left(x+\pi \right)=-\cos \left(x\right)=-\left(-\sqrt{\frac{8}{9} } \right)=\sqrt{\frac{8}{9} }

  • D'après le cours, on sait que : sin⁡(π−x)=sin⁡(x)\sin \left(\pi -x\right)=\sin \left(x\right)
    Ainsi : sin⁡(π−x)=sin⁡(x)=13\sin \left(\pi -x\right)=\sin \left(x\right)=\frac{1}{3}

  • D'après le cours, on sait que : sin⁡(π2−x)=cos⁡(x)\sin \left(\frac{\pi }{2} -x\right)=\cos \left(x\right)
    Ainsi : sin⁡(π2−x)=cos⁡(x)=−89\sin \left(\frac{\pi }{2} -x\right)=\cos \left(x\right)=-\sqrt{\frac{8}{9} }

  • D'après le cours, on sait que : cos⁡(π2+x)=−sin⁡(x)\cos \left(\frac{\pi }{2} +x\right)=-\sin \left(x\right)
    Ainsi : cos⁡(π2+x)=−sin⁡(x)=−13\cos \left(\frac{\pi }{2} +x\right)=-\sin \left(x\right)=-\frac{1}{3}

  • D'après le cours, on sait que : cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right)
    Ainsi : cos⁡(x+2π)=cos⁡(x)=−89\cos \left(x+2\pi \right)=\cos \left(x\right)=-\sqrt{\frac{8}{9} }